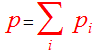Modèle de gaz parfait
Le gaz parfait est un modèle thermodynamique décrivant le comportement des gaz réels[1] à basse pression
Expérimentalement, aux pressions faibles de l'ordre de 1 bar et inférieur à 1 bar les gaz réels se comportent comme des gaz parfaits.
Définition :
Un gaz parfait est constitué d'un ensemble d'atomes ou molécules considérés comme des particules ponctuelles qui n'interagissent pas entre elles. Ce sont les chocs des particules contre les parois du récipient qui sont responsables de la pression exercée par le gaz. Les gaz parfaits obéissent à certaines lois:
[2]La loi de Boyle-Mariotte : à T = cst → P.V = cst P1 . V1 = P2 . V2 ⇒ P1 / V2 =P2 / V1
La loi d'Avogadro : Des volumes égaux de gaz parfait différents, contiennent le même nombre de molécules aux mêmes conditions de température et de pression.
Vm = 22,414 L.mol–1 dans les CNTP (0°C et 1 atm = 101 325 Pa).
Vm = 24,055 L·mol–1 à 20°C sous 1 atm (CHTP).
Loi de Charles : à P = cst →V =α .T→ le volume d'un gaz parfait est proportionnel à sa température. V1 / T1 =V2 / T2
Loi de Gay – Lussac : V = cst →P =α .T→ la pression d'un gaz parfait est proportionnel à sa température. P1 / T1 =P2 / T2
Complément :
Un gaz parfait est un gaz qui satisfait l'équation d'´etat PV = nRT et dont l'´énergie dépend uniquement de la temp´erature (T). Les gaz réels dans les conditions habituelles
satisfont en général ces contraintes de fa¸con approchée (mais pas exactement). En revanche, plus un gaz est dense, moins sa modélisation en terme de gaz parfait est satisfaisante.
Équation d'état d'un gaz parfait
Les variables d'état ne sont pas toutes indépendantes, mais liées entre elles par des équations dites équations d'état du type f (P,V,T,n) : PV=nRT
L'équation qui décrit le comportement d'un gaz considéré comme parfait :pV=nRT
Où :
P : Pression du gaz
V : volume du gaz
n : nombre de moles du gaz
R : constante des gaz parfaits
T : température du gaz
Dans cette équation dite équation d'état des gaz parfaits, chaque variable d'état (pression, volume ou température) dépend des deux autres variables;
D'où : p=f(V,T) ;V=f(p,T) ,T=f(V,p)
Exemple :
Sachant qu'une mole de gaz occupe un volume de 22,4 l dans les conditions normales (T= 0 °C et P = 1atm), calculer la valeur de la constante des gaz parfaist R :
1) Lorsque la pression est mesurée en (atm) et le volume en (l).
2) En système international.
Solution
1) La pression est mesurée en (atm) et le volume en (l) :
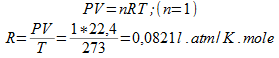
2) En système international :
R=dyne.cm=erg ⇄ R=8.314x107 erg/K.mole
1Joule = 107 erg → R=8.314 J/mole.K
1cal = 4.18 J donc ; R=8.14/4.18 = 1,92 ≈2 cal/mole.K
Mélanges de gaz, pression partielle
Dans un mélange de gaz comprenant n moles (n=∑ ni), chacun d'eux est caractérisé par sa fraction molaire xi.
Pour le gaz i, comprenant ni moles, la fraction molaire xi est donnée par :
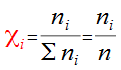
Définition : Pression partielle
La pression partielle pi d'un gaz i dans un mélange de gaz parfait est la pression qu'exercerait ce gaz s'il occupait seul le volume V du récipient (volume total).
Cette pression partielle du gaz est proportionnelle à sa fraction molaire :
![]()
Pi : Pression partielle
Xi : Fraction molaire
PT : Pression totale
Par conséquent la pression totale du mélange est égale à la somme des pressions partielles d'où la loi du Dalton: