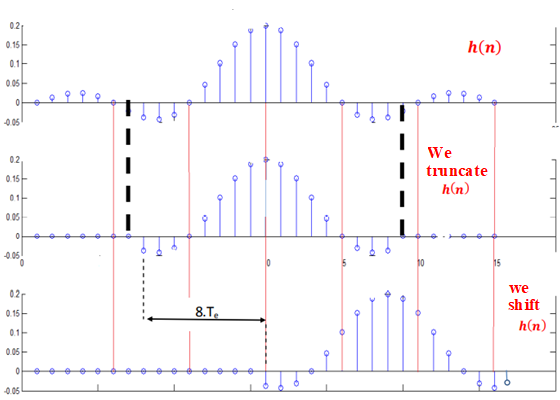
Temporal sampling (impulse invariance)
Let g(t) be the impulse response of the analogue filter :
\(\delta(t)\xrightarrow{\text{ FT}}\bigtriangleup {f}=\int_{-\infty}^{+\infty} \delta(t) e^{-j2πft} \,dx =1\)
\(\xrightarrow{\text{ F i l t e r i n g }}=G(f)= G_{anal}(j\omega)∆(f)=\begin{cases}1 & \quad \text{if } -F_c<fc<F_c \\0 & \quad \text{else } \end{cases}\)
\(\xrightarrow{\text{ Fourier Inverse}}=g(t)= int_{-\infty}^{+\infty} G(f)e^{-j2πft} \,dx=\int_{-F_c}^{F_c} e^{-j2πft} \,dx=2F_c\frac{\sin(2\pi F_ct)}{2\pi F_ct}\)
\(=2F_c\frac{\sin(2\pi F_ct)}{2\pi F_ct}\)
This impulse response is sampled to provide the impulse response of the digital filter :
\(h\left(n\right)=T_eg(nT_e)=2F_cT_e\frac{\sin(2\pi F_cnT_e)}{2\pi F_cnT_e}\)
numerically, we obtain for \(F_c=\frac{F_e}{10}\) :
\(h\left(n\right)=0.2\frac{\sin(n\frac{\pi}{5})}{n\frac{\pi}{5}}\)
Two problems arise :
The impulse response is infinite. To make it finite, we truncate this response using a rectangular window, considering only 17 samples, from n =−8 to n =+8.
The filter is not causal: it responds before the impulse. Therefore, it is not physically feasible. To make it causal (and thus feasible), we shift this response by 8 samples: ℎ(−8) becomes ℎ(0), ℎ(−7) becomes ℎ(1), and so on, until ℎ(8) becomes ℎ(16).
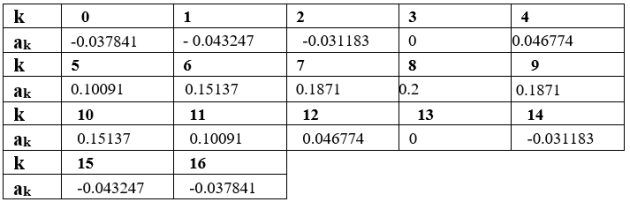
The following page details all the summarized operations. The coefficient values are :
In the table, we observe the property ℎ(k)=h(16−k), and the phase argument varies linearly, indicating an 8-sample delay.