Causal Signal
Consider a real signal \(x\left(t\right)\) with a Fourier transform \(X\left(f\right)\). Given that the signal \(x\left(t\right)\) is real, we can conclude that \(X\left(f\right)\), it possesses Hermitian symmetry.
\(X\left(f\right)=\bar{X}\left(-f\right)\) \(\enspace\) \(\enspace\) \(\enspace\) (37)
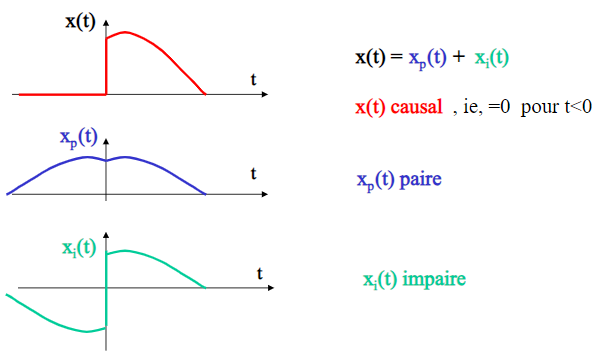
\(x\left(t\right)=x_p\left(t\right)+x_i(t)\) with , \(\left\{\begin{matrix}x_p\left(t\right)=\frac{x\left(t\right)+x\left(-t\right)}{2}\\x_i(t)=\frac{x\left(t\right)-x\left(-t\right)}{2}\\\end{matrix}\right.\) \(\enspace\) \(\enspace\) \(\enspace\) \(\enspace\) (38)
\(x_p\left(t\right)=x_p\left(-t\right)\ \): is the even part of x\left(t\right).
\(x_i\left(t\right)=-x_i(-t)\) : is the odd part of x\left(t\right).
Let the function be,
\(sgn\left(t\right)=\left\{\begin{matrix}1\ \ \ \ \ \ t>0\\-1\ \ \ \ \ t<0\\\end{matrix}\right.\)
It is clear that:
\(x_p\left(t\right)=x_i\left(t\right).sign(t)\ \)and \(x_i\left(t\right)=x_p\left(t\right).sign(t)\ \) \(\enspace\) \(\enspace\) \(\enspace\) (39)