Chapitre 5

Consider a digital system with an impulse response.

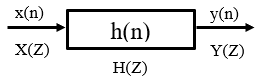
\(y\left(n\right)=x\left(n\right)\ast h(n)\)

\(Y(Z)=X(Z).H(Z)\) \( \Rightarrow\) \(H(Z)=\frac{Y(Z)} {X(Z)}\)(21)

The following equation describes a system :

\(\ \ \ \ \ y\left(n\right)=-\sum_{k=1}^{N}{a_k\ y\left(n-k\right)+\sum_{k=1}^{M}{b_k\ x\left(n-k\right)\ \ \ \Rightarrow }}\)

\(Y\left(Z\right)=-\sum_{k=1}^{N}{a_k\ Z^{-k}\ Y\left(Z\right)+\sum_{k=1}^{M}{b_k\ Z^{-k}X\left(Z\right)}}\) (22)

\(Y\left(Z\right)\left(1+\sum_{k=1}^{N}{a_k\ Z^{-k}\ }\right)=X(Z)\sum_{k=1}^{M}{b_k\ Z^{-k}\ \ }\) (23)

\(H\left(Z\right)=\frac{Y(Z)}{X(Z)}=\frac{\sum_{k=1}^{M}{b_k\ Z^{-k} }}{1+\sum_{k=1}^{N}{a_k\ Z^{-k} }}\) (24)

\(H\left(Z\right)\) is called the transfer function.

\(H\left(Z\right)=\frac{b_0+b_1Z^{-1}+b_2Z^{-2}+\ldots+b_MZ^{-M}}{1+a_1Z^{-1}+a_2Z^{-2}+\ldots+a_NZ^{-N}}\) (25)

With a₀=1

\(H\left(Z\right)=\frac{b_0Z^{-M}\left(Z^M+\left(\frac{b_1}{b_0}\right)Z^{M-1}+\ldots+\frac{b_M}{b_0}\right)}{Z^{-N}\left(Z^N+a_1Z^{N-1}+\ldots+a_N\right)}\)  (26)

\(H\left(Z\right)=\frac{Y(Z)}{X(Z)}=b_0Z^{-\left(M-N\right)}\frac{\prod_{i=1}^{M}\left(Z-Z_i\right)}{\prod_{j=1}^{N}\left(Z-P_j\right)}\) (27)

\(H\left(Z\right)=A\frac{\prod_{i=1}^{M}\left(Z-Z_i\right)}{\prod_{j=1}^{N}\left(Z-P_j\right)}\) (28)

Z_i represents the zeros of \(H\left(Z\right)\)

P_j represents the poles of \(H\left(Z\right)\)

If the a_i are zero : \(a_1=a_2=\ldots=a_N=0\ \ \ \Rightarrow\)

\(H\left(Z\right)=b_0Z^{-M}\prod_{i=1}^{M}\left(Z-Z_i\right)\) (29)

This system is considered to have all zeros, indicating a non-recursive system.

If all coefficients b_i are zero (except \(b_0\neq0\) )

\(H\left(Z\right)=b_0Z^N\frac{1}{\prod_{j=1}^{N}\left(Z-P_j\right)}\) (30)

This system exhibits all Poles, classifying it as a recursive system.