Power Series Expansion
Similar to the inverse transform, we can perform a power series expansion.
Given that \(X(Z)=\frac{N(Z)}{D(Z)}\) , the expansion of X(Z) into a power series in Z-1 involves dividing the numerator by the denominator. The coefficients that weigh Z-1 constitute our x(n).
Example : Example :
1) Consider the Z-transform X(z) of a discrete signal x(k):
\(X\left(z\right)=\frac{0.1\times\ Z\times\left(Z+1\right)}{\left(Z-1\right)^2\times\left(Z-0.6\right)}=\frac{0.1{\ Z}^2+0.1\ Z}{Z^3-2.6{\ Z}^2+2.2\ Z-0.6}\)
We perform the formal division :
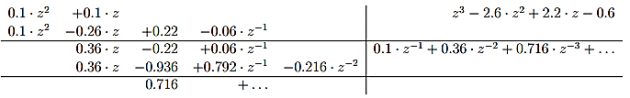
Which directly provides the values of the samples sought:
x(0)=0; x(1)=0.1; x(2)=0.36; x(3)=0.716
2) Determine the inverse Z transform of \(X(Z)=\frac{1-Z^{-1}-5Z^{-2}-3Z^{-3}}{1-3Z^{-1}}\)