Chapitre 5

X(Z) is expressed as the summation of an infinite number of terms, denoted by X(Z) (series). We refer to the set of values of Z for which X(Z) converges as the convergence region of the ZT, denoted by ROC (Region Of Convergence).

To determine this region of convergence, we employ the Cauchy criterion. This criterion asserts that a series has the following form:

\(\sum_{k=0}^{+\infty}{u_k=u_0+u_1+u_2+..\ .}\) Converge \(Si\ \lim\limits_{k \to \infty} \ |U_{k}|^\frac{1}{k}<1\)(10)

We will apply the Cauchy criterion to X(Z) by decomposing the series into two parts:

\(X\left(Z\right)=\sum_{n=-\infty}^{+\infty}{x\left(n\right)Z^{-n}=\sum_{n=-\infty}^{-1}{x\left(n\right)Z^{-n}+\sum_{n=0}^{+\infty}{x\left(n\right)Z^{-n}}}}=X_1\left(Z\right)+X_2\left(Z\right)\)

(11)

The ROC of \(X_2\left(Z\right)\) is determined by :

\(\lim\limits_{x \to \infty} \ |x(n)Z^{-n}|^\frac{1}{n}<1\)

\(\lim\limits_{x \to \infty} \ |x(n)^\frac{1}{n}||Z^{-n}|^\frac{1}{n}<1\)

\(\lim\limits_{x \to \infty} \ |x(n)^\frac{1}{n}|< |Z| \rightarrow |Z|>R_2\) (12)

Then the ROC of \(X_2\left(Z\right)\) is the exterior of a circle with radius R2.

For,

\(X_1(z)= \sum_{n=-\infty}^{-1}x(n)Z^{-n} \quad\) (13)

l=-n

\(X_1\left(Z\right)=\sum_{l=1}^{+\infty}{x\left(-l\right)Z^l}=\sum_{l=0}^{+\infty}{x\left(-l\right)Z^l}-x\left(0\right)\) (14)

\(X_1\left(Z\right)\) converges and \(\lim\limits_{ l \to \infty} \ |x(-l) Z^{ l }|^\frac{1}{ l }<1\)

\(\lim\limits_{ l \to \infty} \ |x(-l) |^ \frac{1}{ l }|Z| <1\)

\(\left|Z\right|<\frac{1}{\lim\limits_{ l \to \infty} \ |x(-l)|^\frac{1}{ l }}\ \ \ \ \ \rightarrow\ \ \ \ \ \left|Z\right|<R_1\)

Then the ROC of \(X_1\left(Z\right)\) East is the interior of a circle of radius R₂.

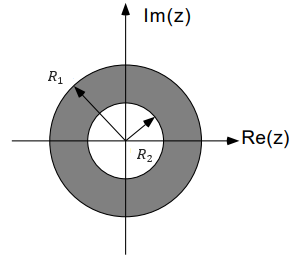
The ROC of \(X\left(Z\right)\) will be the common ROC between that of \(X_1\left(Z\right)\) and \(X_2\left(Z\right)\) , or for this, R1>R2. The ROC of \(X\left(Z\right)\) is a ring on the complex Z plane, bounded by R₂ and R₁, and is given by :

\(R_2<\left|Z\right|<R_1\)