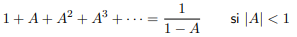The Laplace Transform
\(F\left(p\right)=\int_{-\infty}^{\infty}{f(t)e^{-pt}dt}\) (4)
f(t) represents a continuous signal, and F(p) is the Laplace transform.
For the discrete case, where f(t)=f(nt)
\(f\left(nt\right)\rightarrow F\left(p\right)=\sum_{n=-\infty}^{\infty}{f(nt)e^{-npt}}\) (5)
So \({Z=e}^{pt}\)
\(F(Z)=\sum_{n=-\infty}^{\infty}{f(n)Z^{-n}}\) (6)
We can replace the operator p with its equivalent, \(p=\sigma+j\omega\).
\(Z=e^p=e^\sigma\times \ e^{j\omega}\), where Z is a complex variable that consists of a real part and an imaginary part.
And ∀ n<0, f(n)=0, we speak of a causal signal. Conversely;
For ∀ n>0, f(n)=0, we speak of an anti-causal signal.
For causal signals, we can use the one-sided Z-transform:
\(F(Z)=\sum_{n=0}^{+\infty}{f(n)Z^{-n}}\) (7)
Note : Notation
Let x(n) be a discrete signal.
\(X\left(Z\right)=TZ\left(x\left(n\right)\right)=Z\left(x\left(n\right)\right)\) (8)
\(X\left(Z\right)=\sum_{n=-\infty}^{+\infty}{x(n)Z^{-n}}\) (9)
Example : Example 1 :
Represent the following sequence by its Z-transform:
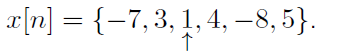
Solution :
X(z) = -7.Z2 + 3.Z1 + Z0 + 4.Z-1 - 8.Z-2 +5Z-3 = -7.Z2 + 3.Z1 + 1 + 4.Z-1 - 8.Z-2 +5.Z-3
Example : Example 2 :
Calculate the Z-transform of the following signal :
\(x(k)= a^k\), \(\forall\ k\geq0\)
The Z-transform is :
\(X\left(Z\right)=\sum_{k=0}^{\infty}{a^k.Z^{-k}}=\sum_{k=0}^{\infty}{\left(a.Z^{-1}\right)^k=\frac{1}{1-a.Z^{-1}}=\frac{Z}{Z-a}}\ \ \ \ si\ \left|a.Z^{-1}\right|<1\)
Note : Reminder :
It is an infinite geometric series.