Shannon's theorem
This theorem states that the correct reconstruction of a signal requires that the sampling frequency Fe be at least twice as large as the highest frequency FM in the signal spectrum :
\(F_e>2F_M\)
When there is spectral overlap, as we have observed, it becomes impossible to correctly reconstruct the signal. However, in most situations, the spectrum of the signal to be sampled is distributed across the entire frequency domain (decreasing towards higher frequencies), but there is no specific frequency Fmax beyond which the energy becomes zero. Therefore, choosing the sampling frequency poses a challenge. In practice, an Fmax is set, beyond which the representation of our signal is deemed satisfactory for the intended applications. Subsequently, a low-pass filter (at Fmax) is applied before sampling to address aliasing. We refer to this type of filter as an anti-aliasing filter.
Example :
Application
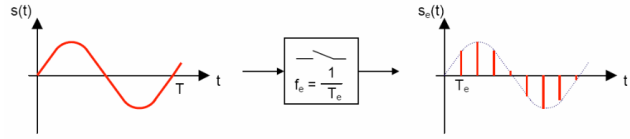
Consider the sinusoidal signal \(s\left(t\right)=sin\left(2\pi Ft\right)\) with period T=1 ms.
Let \(s_e(t)\) be the signal be sampled with a sampling step of Te = 0.1 ms.
Represent the signal s(t) and \(s_e(t)\) for a period T.
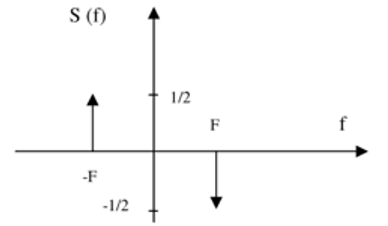
Let S(f) be the Fourier transform of s(t) such that \(S\left(f\right)=\ \frac{1}{2j}\left[\delta\left(f-F\right)-\delta\left(f+F\right)\right]\) .
Represent S(f).
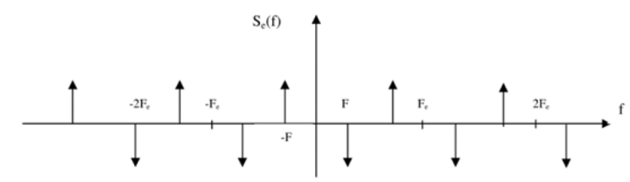
Provide the expression for the Fourier transform \(S_e(f)\) of \(s_e(t)\) .
Represent \(S_e(f)\) for -2 < n ≤ 2.
Answer :
2- a- One has \(S\left(f\right)=\ \frac{1}{2j}\left[\delta\left(f-F\right)-\delta\left(f+F\right)\right] from where S\left(f\right)=\ \frac{1}{2}j\left[\delta\left(f+F\right)-\delta\left(f-F\right)\right]\)
b- the expression of S_e (f) is given by :
\(S_e\left(f\right)=\sum_{n\rightarrow-\infty}^{+\infty}{F_eS\left(f-nf_e\right)}\)
c-