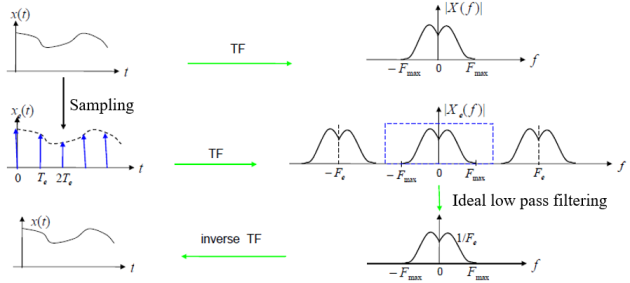
Reconstruction of an Analogue Signal from its Sampled Version
It is well-understood that the sampling operation may result in information loss, especially when the Shannon condition is not satisfied. However, when we meet this condition, we investigate the possibility of reconstructing the signal x(t) through interpolation, ensuring no information loss occurs.
The affirmative answer to this question leads us to the decision to filter the sampled signal using an ideal frequency filter, represented as the rectangular door function ΠFe(t). The output of this filter exhibits the frequency response as the straightforward product of the frequency response of the input (sampled signal) and the filter itself. Under the Shannon condition, where aliasing is absent, we observe the frequency response of the signal s(t) at a multiplicative factor close to \(F_e\).
The problem solution : To reconstruct the signal, simply take the inverse Fourier transform of the basic pattern of \(S_e\left(f\right)\).
Divide by \(F_e\).
Apply ideal low-pass filtering.
Then perform the inverse Fourier transform.
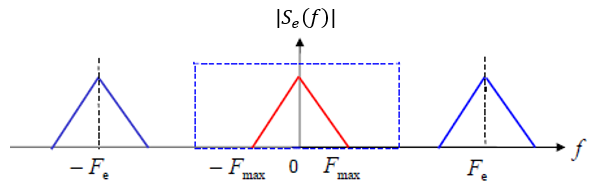
Illustration :
The analogue signal can be reconstructed mathematically, but it can't be done in real life because the ideal low-pass filter doesn't have a causal effect (the impulse response h(t) is anticausal). In other words, the filter is not feasible, and the reconstruction is only approximate.