Inverse Transform
The inverse transform is derived through :

\(X(\omega)=TF^-1{X(\omega)}\)
\(x\left(t\right)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}{X\left(\omega\right)e^{j\omega t}d\omega}\)
Application
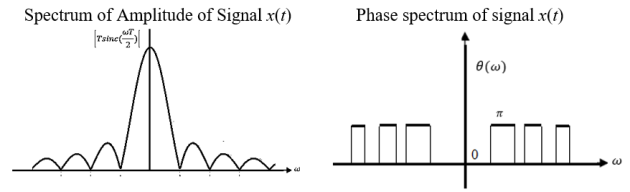
Calculate the Fourier transform of x(t) = rectT(t);
Illustrate the amplitude and phase spectrum of x(t).
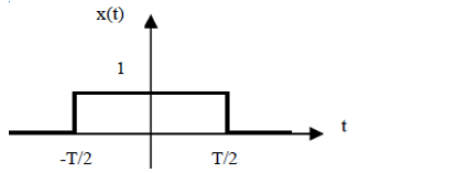
Figure 16: Temporal Representation of a Rectangular Signal.
Correction
1. We apply the definition directly and obtain :
\(X\left(\omega\right)=TF\left\{x(t)\right\}=\int_{-\frac{T}{2}}^{+\frac{T}{2}}{1.e^{-j\omega t}dt}=Tsinc\left(\frac{\omega T}{2}\right)\)
2. representation of X(f) :
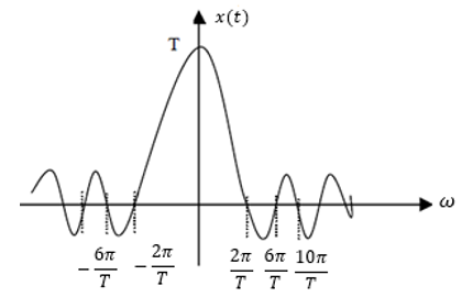
Figure 17: Spectral Representation of a Rectangular Signal.