Signal Processing

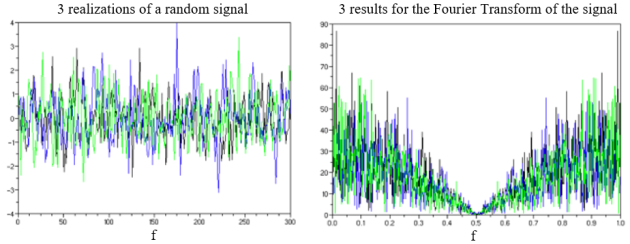
To understand a random process in a meaningful way, statistical analysis is needed, which calls for a lot of realisations (or a long observation period for ergodic signals). Relying on a single realisation is typically insufficient, as it lacks the necessary information on the random process. In fact, calculating the Fourier Transform (TF) of an individual random signal often yields minimal information. Figure 1 illustrates this scenario, depicting the TF calculation for three realisations of the same random phenomenon [13].

We can infer from this that the Fourier Transform (TF) of a random signal lacks distinctive characteristics. What we probably need is to calculate the average of the TFs across a large number of realisations of the same signal. This is a practical solution that we will eventually arrive at, but we are going to explore another path here. We can, in fact, better leverage what we have accomplished so far in the study of random signals. Let's consider that we already possess a statistical tool providing information about the repetition of the signal: the correlation function. This function exhibits characteristic oscillations if the signal contains hidden periodicities and decreases at a speed characteristic of the signal's loss of memory. Therefore, we can assert that the TF of the correlation function could be a promising candidate for obtaining a sort of spectrum of the signal. We anticipate characteristic peaks in its oscillations, and the TF will be narrower as the correlation function extends in time. Let's explore what we can derive from this approach.