Theoretical foundation [14]
The Wiener-Khintchine theorem allowed us to connect the PSD, which we initially defined as the Fourier Transform FT of the correlation function, to the TF of the signal itself. The DSP is exactly as written:
\(S_{xx}(f)= \lim\limits_{T \to \infty}{\frac{1}{T}\left|X_T\left(f\right)\right|^2}\)
This refers to the ratio between the square module of the FT of the signal and its duration, calculated for an infinite duration.
Practically, when we analyze a measurement signal, we will be dealing with a signal of limited duration; all that we can calculate is the magnitude:
\(\frac{1}{T}\left|X_T\left(f\right)\right|^2\)
With T representing the duration of the signal, the Wiener-Khintchine theorem helps us comprehend that the Digital Signal Processing (PSD) is intricately connected to the Fourier Transform (TF) of the signal, akin to power for a deterministic signal. It is the squared magnitude of the TF of the signal that is associated with its power distribution. In the case of a signal of finite duration, the magnitude in equation (5) can serve as an estimator of the Power Spectral Density (PSD).
However, as observed, it may lack significant information, particularly for shorter durations (T not very substantial).
To enhance statistical reliability, an improved approach involves employing an overall average. By averaging \(\frac{1}{T}\left|X_T\left(f\right)\right|^2\) across multiple realisations of the signal, we obtain what is referred to as the periodogram:
\(Periodigram\ = \langle \frac {1} {N}{\lvert X_{T} \rvert}^2 \rangle_{N realisation}\sim S_{xx}(f)\)
The averaging over multiple realisations serves as a partial "compensation" for the finite duration of the recorded signal (assuming ergodicity) and allows for a closer approximation to the theoretical limit of the PSD definition.
Similarly, an effective estimation of the correlation function for a signal recorded with limited duration can be achieved through averaging across several realizations, known as the correlogram:
\(Correlogram\ = \langle \varphi_{xx} \rangle_{N realisation}\sim \varphi_{xx}(t)\)
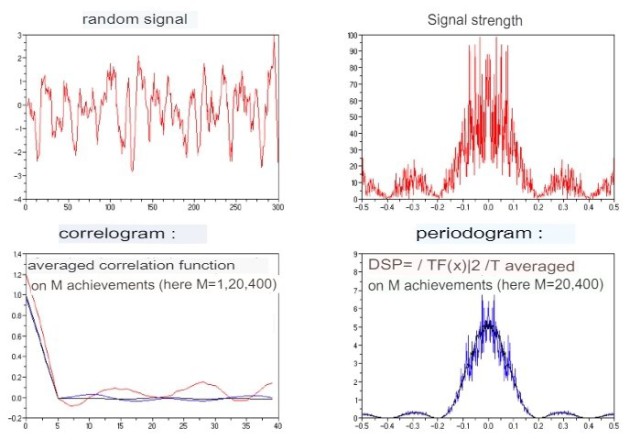
Figure 4 illustrates the application of a periodogram and correlogram to a random signal intentionally designed to incorporate a correlated segment. The impact of increasing the number of realisations is evident, as the estimators progressively converge towards their theoretical limits, manifesting as a triangle function for the correlation function and, consequently, a square cardinal sine for the PSD.