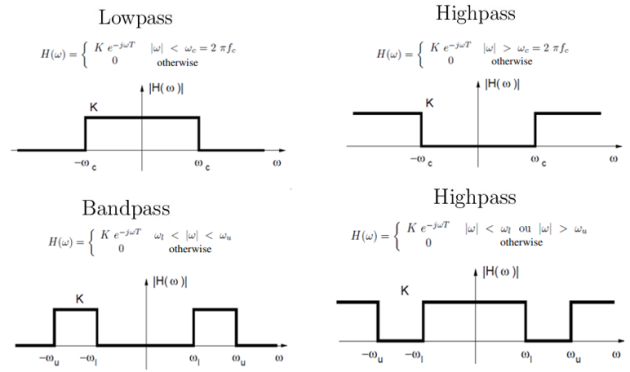
Ideal filters
Ideal filters are characterised by a linear phase shift and are not physically feasible due to their non-causal temporal responses. The ideal frequency responses described above correspond to responses that are not consistent with real-world causal systems.
For instance, considering the low-pass filter with the impulse response :
\(h(t)=K\frac{w_c}{pi}sinc(\frac{w_c}{pi}(t-T)\) , as shown below :
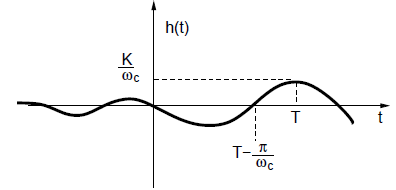
Figure 2 depicts the temporal response of the ideal low-pass filter. It's important to note that part of the signal is not zero for t <0.
This non-causal temporal response is an idealisation that doesn't align with the practical constraints of real-world systems. In practice, physical limitations necessitate the use of approximations and compromises to achieve feasible filter designs with causal responses.
Therefore, the synthesized filters, while not precisely matching the carried frequency, can approximate it. Characteristics that exhibit more or less pronounced differences with respect to the ideal function are mainly the ripples in the passband and attenuated band, as well as the width of the transition. Filters designed for continuous signals (unsampled) typically utilise resistors, self-inductance capacitors, and operational amplifiers.
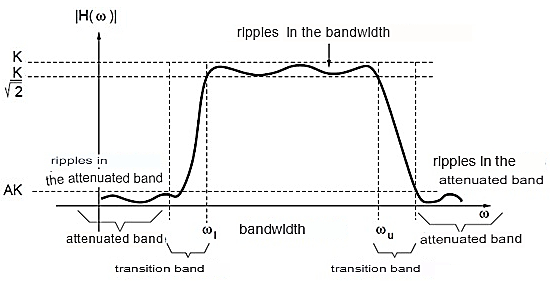
Figure 3 presents the concept and an illustrative example of a real filter's frequency response. This figure aims to provide a visual understanding of how real-world filters deviate from idealised responses, showcasing characteristics such as passband ripples, attenuated bands, and transition width.