Linear Prediction for Speech Processing [12]
A linear predictor utilises past observations of the signal to forecast the next sample of the signal.The following diagram illustrates the structure of such a predictor filter :
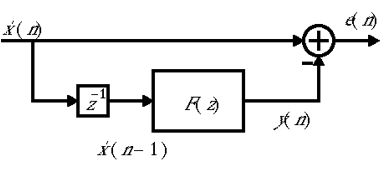
The z-1 operator delays the input signal, x'(n), by one sample.
The operator F(z) represents a filter, and its output y(n) serves as an estimate of the current value of x'(n). Since this block only observes a delayed version of x'(n), its output constitutes a prediction (of x'(n)). The term e(n) denotes the prediction error, representing the difference between the predicted value and the actual signal value.
In qualitative terms, linear prediction leverages the observation that a new sample of a signal is typically not entirely independent of previous samples. This prediction exploits the interdependence between samples. When a predictor performs well, the error signal will consist of samples with weak correlations.
If the input to the linear predictor is the next speech signal, the error signal may not be very intelligible. Thus, the existing relationships between different samples of the signal correlate intelligence (or the associated information).
In practice, for speech signals, the linear predictor must continuously adapt to the spoken content. We segment the input signal into 20 ms segments (160 samples each) and analyze each segment to determine the coefficients of a predictor filter. An algorithm, such as "Burg's algorithm" in the example below, employs one of several existing methods to calculate these predictor filter coefficients every 20 ms.
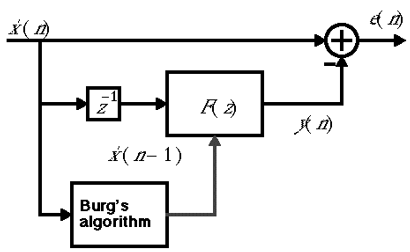
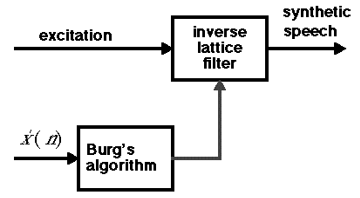
We can test the hypothesis that the intelligibility of a speech signal is associated with the existing correlation between samples by incorporating this correlation into a random signal, such as white noise. We then filter the white noise using the inverse of the predictor filter, generating a prediction error (with parameters updated every 20 ms). The outcome is a speech-like signal that seems to be whispered but remains intelligible. Below is a depiction of the block diagram that generates this synthetic speech: