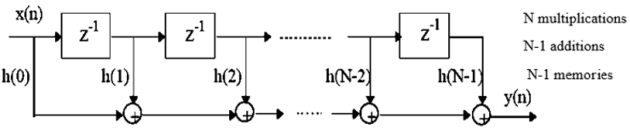
Non-Recursive Filter :
For a finite impulse response filter, where the coefficients a_k are zero, the output y(n) is given by :
\(y\left(n\right)=\sum_{k=1}^{M}{b_k\ x\left(n-k\right)\ }\) (2)
Filters for which the output depends solely on the inputs and not the outputs,
Their response to an impulse is extinguished after a certain time,
They have no analogue equivalent.
A Finite Impulse Response filter (FIR) is a discrete, time-invariant linear system governed by a difference equation, where the output sample y(n) depends only on a specific number of input samples x (not).
The implementation scheme will proceed as follows :
Example : Example
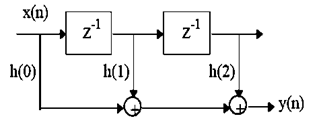
Consider the recurrence equation be \(y\left(n\right)=x\left(n\right)+3x\left(n-1\right)+2x(n-2)\) with impulses responses \(h\left(0\right)=1\), \(h\left(1\right)=3h\) , \(h\left(2\right)=2\).
Its structure is :